Spot the difference:

Python 2.5.2 (r252:60911, Aug  6 2008, 09:17:29) 
[GCC 4.3.1] on linux2
Type "help", "copyright", "credits" or "license" for more information.
>>> import re
>>> def p(string):
...     print re.sub(r'\n +', '\n', string)
... 
>>>
>>> import os
>>> p(os.popen2.__doc__)
Execute the shell command 'cmd' in a sub-process.  On UNIX, 'cmd'
may be a sequence, in which case arguments will be passed directly to
the program without shell intervention (as with os.spawnv()).  If 'cmd'
is a string it will be passed to the shell (as with os.system()). If
'bufsize' is specified, it sets the buffer size for the I/O pipes.  The
file objects (child_stdin, child_stdout) are returned.
>>>
>>> import popen2
>>> p(popen2.popen2.__doc__)
Execute the shell command 'cmd' in a sub-process. On UNIX, 'cmd' may
be a sequence, in which case arguments will be passed directly to the
program without shell intervention (as with os.spawnv()). If 'cmd' is a
string it will be passed to the shell (as with os.system()). If
'bufsize' is specified, it sets the buffer size for the I/O pipes. The
file objects (child_stdout, child_stdin) are returned.
>>> 

It took me a while to realize why my program was failing since I was reading the documentation for one version and using the other :-)

So, despite the occasional mocking from my friends, I continue to write presentations in Latex using prosper and pstricks, hoping that when the time comes I'll be able to save the day. In this case I wanted to create images that exhibit the dining philosophers problem for a presentation about synchronization in multithreading environments.

Here's one that exhibits a deadlock: (L and W stands for Locked and Waiting respectively)

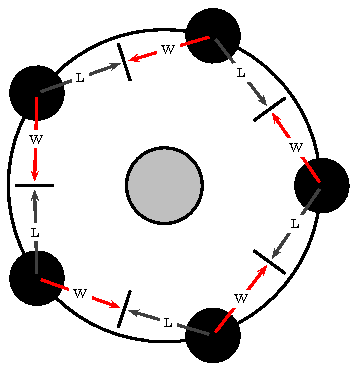
And here's the Latex code:

\listfiles
\documentclass[a4paper]{article}

\usepackage{pstricks}
\usepackage{pst-node}
\usepackage{multido}
\usepackage{calc}

\begin{document}
\definecolor{DarkBlue1}{rgb}{.031,.251,.420}
\begin{pspicture}(12,10)
    \psset{linewidth=2pt}
    
    \pnode(6, 5){O} % center
    \SpecialCoor
    \pscircle[fillcolor=lightgray,fillstyle=solid](O){1}
    \pscircle(O){4}
    
    % philosophers and forks
    \newcounter{degp}
    \newcounter{degf}
    \setcounter{degp}{0}
    \setcounter{degf}{36}
    \multido{\idx=0+1}{5}{
        \addtocounter{degp}{72}
        \addtocounter{degf}{72}
        % Philosophers
        \pscircle[fillcolor=black,fillstyle=solid]([nodesep=4,angle=\arabic{degp}]O){.7}
        \pnode([nodesep=4, angle=\arabic{degp}]O){P\idx}
        % Forks
        \psline([nodesep=3.8, angle=\arabic{degf}]O)([nodesep=2.8, angle=\arabic{degf}]O)
        \pnode([nodesep=3.3, angle=\arabic{degf}]O){F\idx}
    }
    
    % deadlock arrows
    \psset{nodesep=3pt, arrows=->}
    \newcounter{next}
    \newcounter{prev}
    \setcounter{next}{0}
    \setcounter{prev}{0}
    \multido{\idx=0+1}{5}{
        \setcounter{prev}{ (\idx + 4) - ((4 + \idx) / 5)*5}
        % Locked (L) arrow
        \ncline[linecolor=darkgray]{P\idx}{F\arabic{prev}}
        \ncput*{L}
        % Waiting (W) arrow
        \ncline[linecolor=red]{P\idx}{F\idx}
        \ncput*{W}
    }
\end{pspicture}
\end{document}

The special coordinates mode is used (\SpecialCoor), which allows for defining placement by polar coordinates using a node (O in this case) as a reference. Additionally the calc package allows for counter commands that accept infix notation expressions instead of a simple value. (References:calc, pstricks)

One reason I enjoy programming in Python is its great flexibility.

A few months back I was trying to find some kind of security mechanism for accesses in arbitrary Python objects. The idea was that the access mechanism in the object should be independent from the security policy enforcing.

Here is what I did:

class Access(object):
       def __init__(self, access_fn, permissions):
               self.access_fn   = access_fn
               self.permissions = permissions

       def authenticate(self, credentials):
              print "authenticating ..."

       def __call__(self, credentials, arg):
               self.authenticate(credentials)
               return self.access_fn(arg)

The __call__ is a special method name, which is used to create (or emulate) "callable" objects. An instance of an object in which __call__ is defined, can be "called" as a function. So if acc is an instance of the Access class acc(creds, arg) is equivalent to acc.__call__(creds, arg).

For example:

class FooBar(object):
       def __init__(self, foo, bar):
               self.foo = foo
               self.bar = bar

AccessFoo = Access(lambda arg: arg.foo, None)
foobar = FooBar("foo", "bar")
print AccessFoo(None, foobar)

... simple yet powerfull.

Recently I discovered a nice feature of gcc, the constructor function attribute.

I was writing a C program and I wanted to be able to translate a string that was given as an argument at runtime to the address of a specific function, in order to test different implementations.

The problem with my original approach was that I had to add the functions (the pointer and the name) in an array, which was declared in a different file than the body of the functions. That made difficult for me to keep in sync the functions in the array with the declared functions.

Another approach would be to use the dynamic linking loader and find the address of the function via a call to dlsym (3), but this introduces a lot of unnecessary overhead. I didn't want to dynamically load a library, I just wanted to find a symbol by its name. (Note: There is an interesting paper, about shared libraries written by Ulrich Drepper)

The solution I came up with was to use the constrictor function attribute, which causes the function to be called automatically before execution enters main().

Here is some code:

struct method_s {
        char            *name;
        function_t      *fn;
        struct method_s *next;
};
typedef struct method_s method_t;

#define METHOD_INIT(func) \
void __attribute__((constructor)) func ## _init (void) \
{ \
        method_t *method = method_create( #func, func); \
        method_add(method); \
}

Where, method_create allocates and initializes a method and method_add adds the method to a list, with all the available methods. Now all I had to do in order to put a function in the list, was to add a METHOD_INIT(function).

-----

I've been messing around with my (never-finished) web page again. I always liked to be able to seperate content from presentation and the best way to achieve that is by using CSS. Here are some sites with CSS design examples which I found useful:

• Open Source Web Design
• Open Web Design
• CSS Zen Garden

-----

I came upon this wikipedia entry about Raymond Smullyan. In this entry there are links to three articles of him, which I found both amusing and thought provoking:

• Is God a Taoist? by Raymond Smullyan, 1977.
• An Epistemological Nightmare
• Planet Without Laughter by Raymond Smullyan, 1980

-----

From wikipedia:Banksy:

Banksy (born 1975) is a graffiti artist from Bristol, UK, whose artwork has appeared throughout London and other locations around the world. Despite this he carefully manages to keep his real name from the mainstream media. However, many newspapers assert that his real name is Robert or Robin Banks.

Examples of his work:

• From www.banksy.co.uk

  • pissed-tramp.jpg
  • barcode.jpg
  • petagirl2.jpg
  • ballongirl.jpg
  • beachboys_01.jpg
  • feelingbw2.gif

• From www.pbase.com/coolmind/banksy_london

  • www.pbase.com/coolmind/image/22833696
  • www.pbase.com/coolmind/image/22850604
  • www.pbase.com/coolmind/image/22850603
  • www.pbase.com/coolmind/image/31768312
  • www.pbase.com/coolmind/image/24145977

-----

Intro

Let's assume that we have a binary number and we want to find the number of bits that are '1'. This is also known as the hamming weight of the number.

Method 1

One way to do this is illustrated bellow (taken from a friend's code):

int cnz(unsigned long ul)
{
        int nrbits = 0;

        for (;;){
                if (!ul) break;
                ul &= (ul -1);
                nrbits++;
        }

        return nrbits;
}

This algorithm takes advantage of the fact that the (ul-1) operation reverses all the bits of the ul until (and including) the first '1' reached starting from the end. Using this algorithm we need a number of steps equal to the number of '1'.

Method 2

Linux kernel on the other hand uses the following method (assuming for our example that the size of our number is 32 bits):

unsigned int generic_hweight32(unsigned int w)
{
        unsigned int res = w;

        res = (res & 0x55555555) + ((res >>  1) & 0x55555555);
        res = (res & 0x33333333) + ((res >>  2) & 0x33333333);
        res = (res & 0x0F0F0F0F) + ((res >>  4) & 0x0F0F0F0F);
        res = (res & 0x00FF00FF) + ((res >>  8) & 0x00FF00FF);
        res = (res & 0x0000FFFF) + ((res >> 16) & 0x0000FFFF);

        return res;
}

Note that:

 0x55555555 is 01010101010101010101010101010101
 0x33333333 is 00110011001100110011001100110011
 0x0F0F0F0F is 00001111000011110000111100001111
 0x00FF00FF is 00000000111111110000000011111111
 0x0000FFFF is 00000000000000001111111111111111

This method is based on the principle of divide and conquer. Given that our initial number is represented as: a₀a₁a₂...a₃₁ It works like this:

• step 1: a₀a₁ = a₀ + a₁ ... a₃₀a₃₁ = a₃₀ + a₃₁
• step 2: a₀a₁a₂a₃ = a₀a₁ + a₂a₃ ... a₂₈a₂₉a₃₀a₃₁ = a₂₈a₂₉ + a₃₀a₃₁
• ...
• step 5 : a₀...a₃₁ = a₀...a₁₅+a₁₆...a₃₂

Note that the steps of the algorithm are log₂(total_nr_bits) for the general case.

-----